En matemáticas, una serie de Taylor de una función f(x) infinitamente derivable (real o compleja) definida en un intervalo abierto (a-r, a+r) se define como la siguiente suma:
Definición
La serie de Taylor de una función f de números reales o complejos que es infinitamente diferenciable en un entorno de números reales o complejos a, es la serie de potencias:
Series de Maclaurin (Taylor alrededor de 0) notables
A continuación se enumeran algunas series de Taylor de funciones básicas. Todos los desarrollos son también válidos para valores complejos de x.
Función exponencial y logaritmo natural
Serie geométrica
Teorema del binomio
y cualquierpara
 complejo
complejoFunciones trigonométricas
-
- Donde Bs son los Números de Bernoulli.
Funciones hiperbólicas
Función W de Lambert
Varias variables
La serie de Taylor se puede generalizar a funciones de d variables: es un coeficiente multinomial. Como ejemplo, para una función de 2 variables, x e y, la serie de Taylor de segundo orden en un entorno del punto (a, b) es:
es un coeficiente multinomial. Como ejemplo, para una función de 2 variables, x e y, la serie de Taylor de segundo orden en un entorno del punto (a, b) es: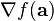 es el gradiente y
es el gradiente y 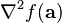 es la matriz hessiana. Otra forma:
es la matriz hessiana. Otra forma:Aplicaciones
Además de la obvia aplicación de utilizar funciones polinómicas en lugar de funciones de mayor complejidad para analizar el comportamiento local de una función, las series de Taylor tienen muchas otras aplicaciones.Algunas de ellas son: análisis de límites y estudios paramétricos de los mismos, estimación de números irracionales acotando su error, teorema de L'Hopital para la resolución de límites indeterminados, estudio de puntos estacionarios en funciones (máximos o mínimos relativos o puntos sillas de tendencia estrictamente creciente o decreciente), estimación de integrales, determinación de convergencia y suma de algunas series importantes, estudio de orden y parámetro principal de infinitésimos, etc.
Referencias
- ↑ Kline, M. (1990) Mathematical Thought from Ancient to Modern Times. Oxford University Press. pp. 35-37.
- ↑ Boyer, C. and Merzbach, U. (1991) A History of Mathematics. John Wiley and Sons. pp. 202-203.
- ↑ «Neither Newton nor Leibniz - The Pre-History of Calculus and Celestial Mechanics in Medieval Kerala». MAT 314. Canisius College


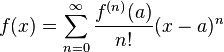




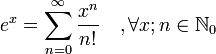


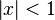

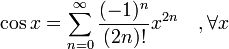











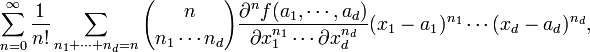
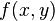

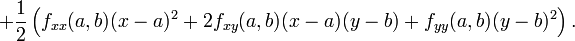
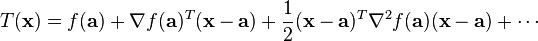

No hay comentarios.:
Publicar un comentario