El área es una medida de la extensión de una superficie, expresada en unidades de medida denominadas superficiales. Para superficies planas el concepto es más intuitivo. Cualquier superficie plana de lados rectos puede triangularse y se puede calcular su área como suma de las áreas de dichos triángulos. Ocasionalmente se usa el término "área" como sinónimo de superficie, cuando no existe confusión entre el concepto geométrico en sí mismo (superficie) y la magnitud métrica asociada al concepto geométrico (área).
Sin embargo, para calcular el área de superficies curvas se requiere introducir métodos de geometría diferencial.
Para poder definir el área de una superficie en general –que es un concepto métrico–, se tiene que haber definido un tensor métrico sobre la superficie en cuestión: cuando la superficie está dentro de un espacio euclídeo, la superficie hereda una estructura métrica natural inducida por la métrica euclídea.
Área de superficies curvas
El área de una superficie curva es más complejo y en general supone realizar algún tipo de idealización o límite para medirlo.
- Cuando la superficie es desarrollable, como sucede con el área lateral de un cilindro o de un cono el área de la superficie puede calcularse a partir del área desarrollada que siempre es una figura plana. Unacondición matemática necesaria para que una superficie sea desarrollable es que su curvatura gaussiana sea nula.
- Cuando la superficie no es desarrollable, el cálculo de la superficie o la fórmula analítica para encontrar dicho valor es más trabajoso. Un ejemplo de superficie no desarrollable es la esfera ya que su curvatura gaussiana coincide con el inverso de su radio al cuadrado, y por tanto no es cero. Sin embargo la esfera es una superficie de revolución.
Superficie de revolución
Cuando una superficie curva puede ser generada haciendo girar un curva plana o generatriz alrededor de un eje directriz, la superficie resultante se llama superficie de revolución y su área puede ser calculada fácilmente a partir de la longitud de la curva generatriz que al girar conforma la superficie. Si y=f(x) es la ecuación que define un tramo de curva, al girar esta curva alrededor del eje X se genera una superficie de revolución cuya área lateral vale:
Ejemplos particulares de superficies de revolución son:
- El área de esfera de radio R que viene dada por
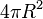
- El área de un cono de radio R y de altura h viene dada por
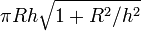
- El área lateral de un cilindro de radio R y altura h es simplemente
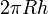
Cálculo general de áreas
Mediante la geometría diferencial de superficies o más generalmente la geometría riemanniana puede calcularse el área de cualquier superficie curva finita. Si la superficie viene dada por la función explícita z = f(x, y) entonces, dada una región Ω contenida en una superficie su área resultar ser:
De manera un poco más general si conocemos la ecuación paramétrica de la superficie en función de dos coordenadas cualesquiera u y v entonces el área anterior puede escribirse como:
Donde E, F y G son las componentes del tensor métrico o primera forma fundamental de la superificie en las coordenadas paramétricas u y v.

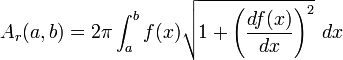

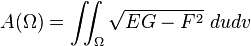
No hay comentarios.:
Publicar un comentario